塑料内存

2019-12-01发表2026-03-08更新中间件 / 缓存13 分钟读完 (大约1951个字)

缓存分类

在我们日常开发中，常见的缓存主要就是静态缓存、分布式缓存和热点本地缓存这三种。

静态缓存在 Web 1.0 时期是非常著名的，它一般通过生成 Velocity 模板或者静态 HTML 文件来实现静态缓存，在 Nginx 上部署静态缓存可以减少对于后台应用服务器的压力。例如，我们在做一些内容管理系统的时候，后台会录入很多的文章，前台在网站上展示文章内容，就像新浪，网易这种门户网站一样。

当然，我们也可以把文章录入到数据库里面，然后前端展示的时候穿透查询数据库来获取数据，但是这样会对数据库造成很大的压力。即使我们使用分布式缓存来挡读请求，但是对于像日均 PV 几十亿的大型门户网站来说，基于成本考虑仍然是不划算的。

所以我们的解决思路是每篇文章在录入的时候渲染成静态页面，放置在所有的前端 Nginx 或者 Squid 等 Web 服务器上，这样用户在访问的时候会优先访问 Web 服务器上的静态页面，在对旧的文章执行一定的清理策略后，依然可以保证 99% 以上的缓存命中率。

这种缓存只能针对静态数据来缓存，对于动态请求就无能为力了。那么我们如何针对动态请求做缓存呢？这时你就需要分布式缓存了。

分布式缓存的大名可谓是如雷贯耳了，我们平时耳熟能详的 Memcached、Redis 就是分布式缓存的典型例子。它们性能强劲，通过一些分布式的方案组成集群可以突破单机的限制。所以在整体架构中，分布式缓存承担着非常重要的角色。

对于静态的资源的缓存你可以选择静态缓存，对于动态的请求你可以选择分布式缓存，那么什么时候要考虑热点本地缓存呢？

**答案是当我们遇到极端的热点数据查询的时候。**热点本地缓存主要部署在应用服务器的代码中，用于阻挡热点查询对于分布式缓存节点或者数据库的压力。

比如某一位明星在微博上有了热点话题，“吃瓜群众”会到他 (她) 的微博首页围观，这就会引发这个用户信息的热点查询。这些查询通常会命中某一个缓存节点或者某一个数据库分区，短时间内会形成极高的热点查询。

那么我们会在代码中使用一些本地缓存方案，如 HashMap，Guava Cache 或者是 Ehcache 等，它们和应用程序部署在同一个进程中，优势是不需要跨网络调度，速度极快，所以可以来阻挡短时间内的热点查询。来看个例子。

比方说你的垂直电商系统的首页有一些推荐的商品，这些商品信息是由编辑在后台录入和变更。你分析编辑录入新的商品或者变更某个商品的信息后，在页面的展示是允许有一些延迟的，比如说 30 秒的延迟，并且首页请求量最大，即使使用分布式缓存也很难抗住，所以你决定使用 Guava Cache 来将所有的推荐商品的信息缓存起来，并且设置每隔 30 秒重新从数据库中加载最新的所有商品。

首先，我们初始化 Guava 的 Loading Cache：

CacheBuilder<String, List<Product>> cacheBuilder = CacheBuilder.newBuilder().maximumSize(maxSize).recordStats(); // 设置缓存最大值
cacheBuilder = cacheBuilder.refreshAfterWrite(30, TimeUnit.Seconds); // 设置刷新间隔
 
LoadingCache<String, List<Product>> cache = cacheBuilder.build(new CacheLoader<String, List<Product>>() {
    @Override
    public List<Product> load(String k) throws Exception {
        return productService.loadAll(); // 获取所有商品
    }
});

这样，你在获取所有商品信息的时候可以调用 Loading Cache 的 get 方法，就可以优先从本地缓存中获取商品信息，如果本地缓存不存在，会使用 CacheLoader 中的逻辑从数据库中加载所有的商品。

由于本地缓存是部署在应用服务器中，而我们应用服务器通常会部署多台，当数据更新时，我们不能确定哪台服务器本地中了缓存，更新或者删除所有服务器的缓存不是一个好的选择，所以我们通常会等待缓存过期。因此，这种缓存的有效期很短，通常为分钟或者秒级别，以避免返回前端脏数据。

缓存的不足

通过了解上面的内容，你不难发现，缓存的主要作用是提升访问速度，从而能够抗住更高的并发。那么，缓存是不是能够解决一切问题？显然不是。事物都是具有两面性的，缓存也不例外，我们要了解它的优势的同时也需要了解它有哪些不足，从而扬长避短，将它的作用发挥到最大。

**首先，缓存比较适合于读多写少的业务场景，并且数据最好带有一定的热点属性。**这是因为缓存毕竟会受限于存储介质不可能缓存所有数据，那么当数据有热点属性的时候才能保证一定的缓存命中率。比如说类似微博、朋友圈这种 20% 的内容会占到 80% 的流量。所以，一旦当业务场景读少写多时或者没有明显热点时，比如在搜索的场景下，每个人搜索的词都会不同，没有明显的热点，那么这时缓存的作用就不明显了。

**其次，缓存会给整体系统带来复杂度，并且会有数据不一致的风险。**当更新数据库成功，更新缓存失败的场景下，缓存中就会存在脏数据。对于这种场景，我们可以考虑使用较短的过期时间或者手动清理的方式来解决。

**再次，之前提到缓存通常使用内存作为存储介质，但是内存并不是无限的。**因此，我们在使用缓存的时候要做数据存储量级的评估，对于可预见的需要消耗极大存储成本的数据，要慎用缓存方案。同时，缓存一定要设置过期时间，这样可以保证缓存中的会是热点数据。

**最后，缓存会给运维也带来一定的成本，**运维需要对缓存组件有一定的了解，在排查问题的时候也多了一个组件需要考虑在内。

虽然有这么多的不足，但是缓存对于性能的提升是毋庸置疑的，我们在做架构设计的时候也需要把它考虑在内，只是在做具体方案的时候需要对缓存的设计有更细致的思考，才能最大化的发挥缓存的优势。

2019-11-20发表2026-03-08更新算法 / 排序3 分钟读完 (大约379个字)

LeetCode两个经典的排序算法

这回是标题党，记录下两个分而治之的排序算法（手写），分而治之的算法很容易改造成并行算法，肯定是未来的潮流， leetcode已通过，两个算法都使用了原地(inplace)更新。

class Solution {
    public List<Integer> sortArray(int[] nums) {
        // merge(nums, 0, nums.length - 1);
        sort(nums, 0, nums.length - 1);
        return IntStream.of(nums).boxed().collect(Collectors.toList());
    }

	//-------------------归并排序-------------------//
    private void merge(int[] nums, int start, int end) {
        if (start >= end) return;
        int midIdx = start + (end - start) / 2;
        merge(nums, start, midIdx);
        merge(nums, midIdx+1, end);
        concat(nums, start, midIdx, end);
    }

    private void concat(int[] nums, int start, int midIdx, int end) {
        int[] tmp = new int[end - start + 1];
        int lp = start, rp = midIdx + 1, i = 0;

        while (lp <= midIdx && rp <= end) {
            tmp[i++] = nums[lp] < nums[rp] ? nums[lp++] : nums[rp++];
        }

        while (lp <= midIdx) {
            tmp[i++] = nums[lp++];
        }

        while (rp <= end) {
            tmp[i++] = nums[rp++];
        }

        System.arraycopy(tmp, 0, nums, start, tmp.length);
    }

    // -------------------  归并排序 链表 ---------------------//

    class Solution {
        public ListNode mergeKLists(ListNode[] lists) {
            if (lists.length == 0) return null;
            return merge(lists, 0 , lists.length - 1);
        }

        private ListNode merge(ListNode[] lists, int low, int high) {
            if (low == high) return lists[low];

            int mid = (high - low) / 2 + low;

            return mergeLists( merge(lists, low, mid), merge(lists, mid+1, high));
        }

        public ListNode mergeLists(ListNode node1, ListNode node2) {
            if (node1 == null) return node2;
            if (node2 == null) return node1;

            if (node1.val < node2.val) {
                node1.next = mergeLists(node1.next, node2);
                return node1;
                
            } else {
                node2.next = mergeLists(node1, node2.next);
                return node2;
            }
        }
    }
    
    //-------------------快速排序-------------------//

    private void sort(int[] nums, int start, int end) {
        if (start >= end) return;

        int bIdx = partition(nums, start, end);
        sort(nums, start, bIdx - 1);
        sort(nums, bIdx + 1, end);
    }

    private int partition(int[] nums, int start, int end) {
        int idx = start, base = nums[end];

        for (int i = start; i < end; i++) {
            if (nums[i] < base) {
                swap(nums, idx++, i);
            }
        }
        swap(nums, idx, end);
        return idx;
    }

    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

2019-09-24发表2026-03-08更新工作 / 总结4 分钟读完 (大约615个字)

季度总结如何管理自我时间

计划和休息

《软技能》中作者是如何做计划的？

季度计划明确宏观目标，以及如何实现
月计划估算当月能完成多少工作量
周计划为每周安排必须完成的强制性任务
日计划排除干扰，按需调整
休息每隔一段时间休息，只做强制性任务

很惭愧，工作刚开始一两年我少有计划，单纯凭借好奇心学习到了不少东西。大约从去年写年度总结开始才刚刚做一些计划。目前我使用微软to-do跟踪自己的计划进度和deadline效果显著，治好了我的拖延症。

简单来说《软技能》中阐述的几个观点我感觉十分受益：

要有计划
完成计划时保持专注
使用番茄工作法可以保证保证一段时间的专注，同时还可以确定自己的工作效率，总结不足提高自身效率，从而帮助自己精确且高效的指定计划
只有你完成了计划的工作，接下来的休息时间才能安心

这边年读书情况

这半年看的书比较少，但是刷题和博客总结写的多了些

技术类：
《sql反模式》推荐，应该叫数据库结构设计的最佳实践
《软技能，代码之外的生存指南》有很多事比代码更重要的多，推荐

心理类：
《你的灯亮着吗》解决问题前，先要搞清楚问题的本质。一般般

2019-08-10发表2026-03-08更新算法 / 字符串1 分钟读完 (大约147个字)

LeetCode 最长回文子串算法

Manacher 算法容易理解，实现起来也没什么大坑，复杂度还是 O(n)的，花半个小时实现下很有意思

class Solution {
    public String longestPalindrome(String s) {        
        StringBuilder sb = new StringBuilder(2 + 2 * s.length());
        sb.append("^");
        for (int i = 0; i < s.length(); i++) {
            sb.append("#").append(s.charAt(i));
        }
        sb.append("#$");
        
        String s2 = sb.toString();
        
        int maxStart = 1, max = 0, rC = 1, rR = 1;
        int[] p = new int[s2.length()];
        
        for (int i = 1; i < s2.length() - 1; i++ ) {
            
            p[i] = i < rR ? Math.min(p[2 * rC - i], rR - i) : 0;
            
            while (s2.charAt(i+p[i]+1) == s2.charAt(i - p[i] - 1)) {
                p[i] = p[i]+1;
            }
            
            if (i + p[i] > rR) {
                rC = i;
                rR = i + p[i];
            }
            
            if (p[i] > max) {
                maxStart = i - p[i];
                max = p[i];
            }
        }
        

        return s2.substring(maxStart,maxStart + 2*max+1).replace("#", "");
    }
}

2019-07-29发表2026-03-08更新工作 / 挑战3 分钟读完 (大约428个字)

[项目] 多角色权限展示数据的一种实现

多角色权限如果遇到不同角色能看到不同的列可以怎么做

逐行读取

最简单的解决方法，实现简单。但是在微服务中调用接口次数太多，性能很差。

批量读取

实现较复杂，但是性能好很多，下面主要介绍这种方法的思路

批量读取

以分页读取数据为例：

读取第一页数据，包含需要展示数据的id和所属权限（多个）

为什么需要所属权限这个字段呢？因为决定能否看到这行是有你所拥有的所有权限决定的，而决定能否看到哪个列是由这行所拥有的权限决定的。

如何获取该行所拥有的权限呢，我的做法是分不同的权限查询结果通过union 组合起来

将第一页数据原始顺序保存，然后按行拥有权限分组

记录原始顺序是因为后面分组后会打乱，为什么要分组？分组后同样的查询才能聚合在一起，可以简化代码

根据权限分组多次查询所需要的字段，然后将查询结果合并

这里我使用的graphql来选择需要查询的字段

最后还原成原来的顺序

可以使用guava Ordering工具类方便生成Compartor

[]: https://blog.yamato.moe/2018/11/06/2018-11-06-biz/ “根据权限查询时避免角色切换的一种思路”
[]: https://blog.yamato.moe/2019/04/04/Mybatis%20ResultSetHandler_2019-04-04%20%E7%BB%AD/ “【片段】 Mybatis ResultSetHandler 实践-续”
[]: https://blog.yamato.moe/2019/01/09/Mybatis%20ResultSetHandler_2019-01-09/ “【片段】 Mybatis ResultSetHandler 实践”

2019-06-15发表2026-03-08更新算法 / 二叉树15 分钟读完 (大约2235个字)

LeetCode二叉树基础算法

树的高度

104. Maximum Depth of Binary Tree (Easy)

递归计算二叉树左右两边深度，取最大值。


/**

 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        return Math.max(left, right) + 1;
    }
}

平衡树

110. Balanced Binary Tree (Easy)

递归遍历二叉树左右子树深度

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    
    private boolean balance = true;
    
    public boolean isBalanced(TreeNode root) {
        visitTree(root);
        return balance;
    }
    
    private int visitTree(TreeNode root) {
        if (root == null) return 0;
        int left = visitTree(root.left);
        int right = visitTree(root.right);
        if (Math.abs(left - right) > 1 ) this.balance = false;
        return Math.max(left, right) + 1;
    }
}

两节点的最长路径

543. Diameter of Binary Tree (Easy)

递归遍历二叉树左右子树深度，路径就是两边子树深度之和

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    
    private int max;
        
    public int diameterOfBinaryTree(TreeNode root) {
        deep(root);
        return max;
    }
    
    private int deep(TreeNode root) {
        if (root == null) return 0;
        int left = deep(root.left);
        int right = deep(root.right);
        max = Math.max(max,left+right);
        return Math.max(left, right) + 1;
    }
}

翻转树

226. Invert Binary Tree (Easy)

递归交换左右子树的引用

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return root;
        TreeNode right =root.right;
        root.right = invertTree(root.left);
        root.left = invertTree(right);
        return root;
    }
}

归并两棵树

617. Merge Two Binary Trees (Easy)

递归时如果其中一个节点是空，可以直接复用该节点。如果新建节点，需要拷贝节点的左右子树引用，递归时会用到。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        if (t1 == null && t2 == null ) return null;
        if (t1 == null) return t2;
        if (t2 == null) return t1;
        TreeNode root =  new TreeNode(t1.val + t2.val);
        root.left = mergeTrees(t1.left, t2.left);
        root.right = mergeTrees(t1.right, t2.right);
        return root;
    }
}

判断路径和是否等于一个数

Leetcode : 112. Path Sum (Easy)

递归查询子树和是否等于目标和

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) return false;
        if (root.val == sum && root.left == null && root.right == null) return true;
        return  hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
    }
}

统计路径和等于一个数的路径数量

437. Path Sum III (Easy)

双层递归

以当前节点为起点统计路径和
当前节点以下节点为起点统计路径和

以root为根节点的路径数量= 以root为起点统计路径和+root左节点为起点统计路径和+root右节点为起点统计路径和

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int pathSum(TreeNode root, int sum) {
        if (root == null) return 0;
        //结果数 等于 以当前root为父节点和 root以下为父节点结果数之和
        return sum(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum);
    }
    // 计算以当前node为父节点能都多少路径数
    private int sum(TreeNode node, int sum) {
        if (node == null) return 0;
        int count = 0;
        if (node.val == sum) count++;
        count += sum(node.left, sum - node.val) + sum(node.right, sum - node.val);
        return count;
    }
}

子树

572. Subtree of Another Tree (Easy)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSubtree(TreeNode s, TreeNode t) {
        if (s == null) return false;
        return isSubRoot(s, t) || isSubtree(s.left, t) || isSubtree(s.right, t);
    }
    
    public boolean isSubRoot(TreeNode node, TreeNode t) {
        if (node == null && t == null) return true;
        if (node == null || t == null) return false;
        if (node.val != t.val) return false;
        return isSubRoot(node.left, t.left) && isSubRoot(node.right, t.right); 
    }
}

树的对称

101. Symmetric Tree (Easy)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) return true;
        return isSymmetric(root.left, root.right);
    }
    
    public boolean isSymmetric(TreeNode left, TreeNode right) {
        if (left == null && right == null) return true;
        if (left == null || right == null) return false;
        if (left.val != right.val) return false;
        return isSymmetric(left.left, right.right) && isSymmetric(left.right, right.left);
    }
}

最小路径

111. Minimum Depth of Binary Tree (Easy)

和最大路径类似

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) return 0;
        int left = minDepth(root.left);
        int right = minDepth(root.right);
        if (left == 0 || right == 0) return left + right + 1;
        return Math.min(left, right) + 1;
    }
}

统计左叶子节点的和

404. Sum of Left Leaves (Easy)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {

    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;
        if (root.left != null && root.left.left == null && root.left.right == null) return root.left.val + sumOfLeftLeaves(root.right);
        return sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
    }
}
````

#### 相同节点值的最大路径长度

[687. Longest Univalue Path (Easy)](https://leetcode.com/problems/longest-univalue-path/)

递归查找左右子树相同节点值最大路径，最大路径的计算：如果相等路径+1，如果不相等置为0。

```java
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private int path = 0;
    
    public int longestUnivaluePath(TreeNode root) {
        visit(root);
       return path; 
    }
    
    private int visit(TreeNode root) {
        if  (root == null) return 0;
        int left = visit(root.left);
        int right = visit(root.right);
        
        left =  (root.left != null && root.val == root.left.val) ? left + 1 : 0;
        right = (root.right != null && root.val == root.right.val)? right + 1 : 0;
        path = Math.max(path, left+right);
        return Math.max(left, right );
    }
}

间隔遍历

337. House Robber III (Medium)

递归查询两种情况

如果从当前节点开始
从当前节点的子节点开始

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int rob(TreeNode root) {
        if (root == null) return 0;
        int val1 = root.val, val2 = 0;
        if (root.left != null) val1+= rob(root.left.left) + rob(root.left.right);
        if (root.right != null) val1+= rob(root.right.left) + rob(root.right.right);
        
        val2 = rob(root.left) + rob(root.right);
        return Math.max(val1, val2);
    }
}

找出二叉树中第二小的节点

Second Minimum Node In a Binary Tree (Easy)

第二小节点在子树节点上，如果子树值与根节点相等，继续向下查找

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int findSecondMinimumValue(TreeNode root) {
        if (root == null) return -1;
        if (root.left == null) return -1;
        int left = root.left.val, right = root.right.val;
        if (root.val == root.left.val) left = findSecondMinimumValue(root.left);
        if (root.val == root.right.val) right = findSecondMinimumValue(root.right);
        if (left != -1 && right != -1) return Math.min(left, right);
        if (left > -1) return left;
        return right;
    }
}

二叉树的层平均值

637. Average of Levels in Binary Tree (Easy)

BFS

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> ret = new ArrayList<>();
        if (root == null) return ret;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()) {
            int count = queue.size();
            double sum = 0d;
            
            for(int i = 0; i < count; i++) {
                TreeNode node = queue.poll();
                sum+= node.val;
                if (node.left != null) queue.add(node.left);
                if (node.right != null) queue.add(node.right);
            }
            ret.add(sum/count);
        }
        return ret;
    }
}

找树左下角的值

513. Find Bottom Left Tree Value (Easy)

DFS

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private int val = 0;
    
    public int findBottomLeftValue(TreeNode root) {
        if (root == null) return val;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()) {
            // 这一行的数量
            int count = queue.size();
            
            for (int i = 0; i < count; i++) {
                TreeNode node = queue.poll();
                if(i == 0) val = node.val;
                if (node.left != null) queue.add(node.left);
                if (node.right != null) queue.add(node.right);
            }
        }
        return val;
    }
}

非递归实现二叉树的后序遍历

入栈条件：未访问过该节点
出栈条件：访问过该节点

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    
    private List<Integer> res = new LinkedList<>();
    private Stack<TreeNode> stack = new Stack<>();
    private Set<TreeNode> visited = new HashSet<>();
    
    public List<Integer> postorderTraversal(TreeNode root) {
        if (root == null) return res;
        stack.push(root);
        
        while (!stack.isEmpty()) {
            TreeNode node = stack.peek();
            
            if ((node.left == null && node.right == null) || visited.contains(node)) {
                TreeNode i = stack.pop();
                res.add(i.val);
            } else {
                visited.add(node);
                if (node.right != null)
                    stack.push(node.right);
                if (node.left != null) 
                    stack.push(node.left);
            }
        }
        return res;
    }
    
    private void visit(TreeNode root) {
        if(root == null) return;
        visit(root.left);
        visit(root.right);
        res.add(root.val);
    }
}

非递归实现二叉树的前序遍历

入栈条件：无
出栈条件：直接出栈

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private List<Integer> res = new LinkedList<>();
    private Stack<TreeNode> stack = new Stack<>();
    
    public List<Integer> preorderTraversal(TreeNode root) {
        if (root == null) return res;
        stack.push(root);
        
        while (!stack.isEmpty()) {
                TreeNode node = stack.pop();
                res.add(node.val);
                if (node.right != null) stack.push(node.right);
                if (node.left != null)  stack.push(node.left);
        }
        return res;
    }
}

非递归实现二叉树的中序遍历

入栈条件：未访问过该节点
出栈条件：访问过该节点
入栈顺序: right -> middle -> left

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private List<Integer> res = new LinkedList<>();
    private Stack<TreeNode> stack = new Stack<>();
    private Set<TreeNode> visited = new HashSet<>();
    
    public List<Integer> inorderTraversal(TreeNode root) {
        if (root == null) return res;
        push(root);
        
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if ((node.left == null && node.right == null) || visited.contains(node)) {
                res.add(node.val);
            } else {
                push(node);
            }
        }
        return res;
    }
    
    private void push(TreeNode root) {
        if (root == null) return;
        visited.add(root);
        if (root.right != null) stack.push(root.right);
        stack.push(root);
        if (root.left != null) stack.push(root.left);
    }
}

2019-06-15发表2026-03-08更新算法 / 二叉树8 分钟读完 (大约1178个字)

LeetCode 二叉树排序树基础算法

修剪二叉搜索树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode trimBST(TreeNode root, int L, int R) {
        if (root == null) return null;
        if (root.val < L) return trimBST(root.right, L, R);
        if (root.val > R) return trimBST(root.left, L, R);
        root.left = trimBST(root.left, L, R);
        root.right = trimBST(root.right, L, R);
        return root;
    }
}

二叉搜索树中第K小的元素

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private int cnt;
    private int val;
    
    public int kthSmallest(TreeNode root, int k) {
        search(root, k);
        return val;
    
    }
    
    private void search(TreeNode root, int k) {
        if (root == null) return;
        // 
        kthSmallest(root.left, k);
        cnt++;
        if (cnt == k) {
            val =  root.val;
            return;
        }
        kthSmallest(root.right, k);
    }
}

把二叉搜索树转换为累加树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    
    private int sum;
    
    public TreeNode convertBST(TreeNode root) {
        // 中序遍历 但是是从右往左遍历
        // 
        visit(root);
        return root;
    }
    
    
    private void visit(TreeNode root) {
        if (root == null) return;
        
        visit(root.right);
         sum += root.val;
    
        root.val = sum;
        
        visit(root.left);
    }
}

二叉搜索树的最近公共祖先

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 公共祖先在左边
        if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
        // 公共祖先在右边
        if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
        // 公共祖先在这
        return root;
    }
}

二叉树的最近公共祖先

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || p == root || q == root) return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        
        // 左右都是父节点， 上一级就是公共父节点
        if(left != null && right != null) return root;
        if (left == null && right == null) return null;
        if (left != null) return left;
        return right;
    }
}

将有序数组转换为二叉搜索树

二叉树中序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return build(nums, 0, nums.length -1);
    }
    
    
    private TreeNode build(int[] nums, int start, int end) {
        
        if(start> end) return null;
        
        TreeNode node = new TreeNode(nums[(start+end)/2]);
        
        node.left = build(nums, start, (start+end)/2 -1);
        node.right = build(nums, (start+end)/2+1, end);
        return node;
    }
}

有序链表转换二叉搜索树

链表转数组

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        List<Integer> list = new LinkedList();
        ListNode now = head;
        while (now != null) {
            list.add(now.val);
            now = now.next;
        }
        
        return build(list, 0, list.size() - 1);
    }
    
    
    private TreeNode build(List<Integer> nums, int start, int end) {
        
        if(start> end) return null;
        
        TreeNode node = new TreeNode(nums.get((start+end)/2));
        
        node.left = build(nums, start, (start+end)/2 -1);
        node.right = build(nums, (start+end)/2+1, end);
        return node;
    }
}

还可以使用双指针找到链表中间节点，缺点是重复遍历节点

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode sortedListToBST(ListNode head) {
//         List<Integer> list = new LinkedList();
//         ListNode now = head;
//         while (now != null) {
//             list.add(now.val);
//             now = now.next;
//         }
        
//         return build(list, 0, list.size() - 1);
        
        return sortedListToBST(head, null);
        
        

    }
    
    private TreeNode sortedListToBST(ListNode head, ListNode tail) {
        if (head == tail) return null;
        
        ListNode mid = head, end = head;
        while (end != tail && end.next != tail) {
            mid = mid.next;
            end = end.next.next;
        }
        
        TreeNode root = new TreeNode(mid.val);
        root.right = sortedListToBST(mid.next, tail);
        root.left = sortedListToBST(head, mid);
        return root;
    }
    
    
    private TreeNode build(List<Integer> nums, int start, int end) {
        
        if(start> end) return null;
        
        TreeNode node = new TreeNode(nums.get((start+end)/2));
        
        node.left = build(nums, start, (start+end)/2 -1);
        node.right = build(nums, (start+end)/2+1, end);
        return node;
    }
    
}

两数之和 IV - 输入 BST

自己写两次遍历搜索二叉树，注意要排除自身节点

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private boolean res;
    private TreeNode r;
    private TreeNode current;
    
    
    public boolean findTarget(TreeNode root, int k) {
        r = root;
        visit(root, k);
        return res;
    }
    
    private void visit(TreeNode root, int val) {
        if (root == null) return;
        visit(root.left, val);
        current = root;
        if (find(r, val - root.val)) {res = true; return;}
        visit(root.right, val);
    }
    
    private boolean find(TreeNode root, int value) {
        if (root == null) return false;
        if (root == current) return false;
        if (root.val == value ) return true;
        return  (value > root.val) ? find(root.right, value): find(root.left, value);
    }
}

正经思路，中序遍历转化为排序数组，使用双指针查找

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {

    private List<Integer> res = new ArrayList<>(64);
    
    public boolean findTarget(TreeNode root, int k) {

        visitTree(root);
        
        int low = 0, high = res.size() - 1;
        while (low < high) {
            int sum = res.get(low) + res.get(high);
            if (sum == k) return true;
            if (sum < k) low++;
            else high--;
        }
        return false;
        
    }
    

    
    private void visitTree(TreeNode root) {
        if (root == null) return;
        visitTree(root.left);
        res.add(root.val);
        visitTree(root.right);        
    }

}

2019-05-20发表2026-03-08更新Java基础7 分钟读完 (大约1006个字)

IO Modle

操作系统IO模型与Java IO

Java IO模型和操作系统IO模型息息相关，之前阻塞/非阻塞，同步/非同步之间的关系一直分不清，所以很有必要了解下操作系统(linux)提供了哪些接口来进行IO。目前我们只需要了解即可，使用相关可以直接查看java io教程。

最基础的知识

以使用IO读取数据为例，一般操作系统分为两个独立的阶段进行操作：

等待数据准备完成，可以是从磁盘拷贝到内核空间，或者是网卡接受到数据后拷贝到内核空间。
从内核空间将数据拷贝至请求数据的进程。如果是java可能还需从进程拷贝至jvm堆内存。

Blocking I/O Model

这个是最常用的模型，望文生义就是阻塞IO，进行IO的两个阶段会都阻塞程序，直到读取到数据或者返回错误才会返回。

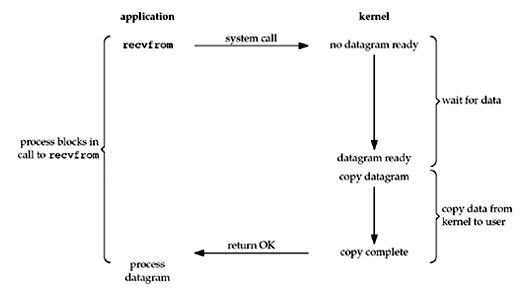
blocking io

具体来说，通过调用系统recvfrom函数，而recvfrom函数会等到出错或者把数据拷贝到进程完成时才会返回。之后我们程序只需要处理错误或者处理数据就可以了。

阻塞模型对应java中绝大部分IO操作，比如网络请求api，io stream api，该模型优点在于简单直观，缺点在长时间阻塞很难支持大量并发IO请求。

Nonblocking I/O Model

该模型在java中没有对应，所以这里只做简单介绍。

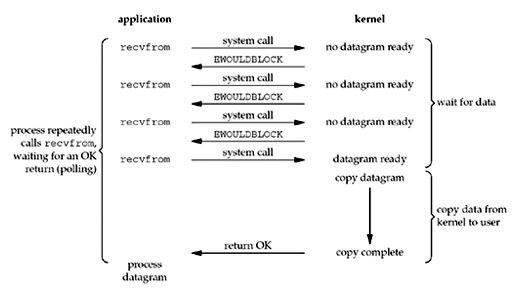
nonblocking io

使用轮询方式调用系统recvfrom函数，recvfrom函数在第一阶段完成前一直返回错误，直到第一阶段完成后，阻塞至第二阶段完成。

这个模型稍显鸡肋，特点是在第一阶段是非阻塞的（进程不会被切换），代码相比阻塞模型来说也更复杂。

I/O Multiplexing Model

非常著名的IO模型，可以支持大量并发IO。通过调用select或者pull并阻塞，而不是在实际调用系统IO时阻塞。使用select阻塞在第一阶段和Blocking I/O的阻塞不太一样，Blocking I/O阻塞在当前IO操作第一阶段，而I/O复用则可以注册多个I/O在select函数，当有一个I/O就绪时select函数就会返回，如果所有I/O处于第一阶段阻塞状态则select函数阻塞。

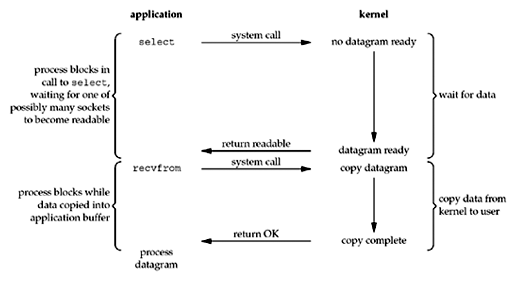
相比较Blocking I/O Model和Nonblocking I/O Model，I/O Multiplexing Model明显能在短时间内处理更多的I/O。如果使用多线程+Blocking I/O Model也能达到类似的效果，但是有可能消耗过多线程资源。

I/O Multiplexing Model对应java NIO的Selector等api

Signal-Driven I/O Model

该模型在java中没有对应，所以这里只做简单介绍。

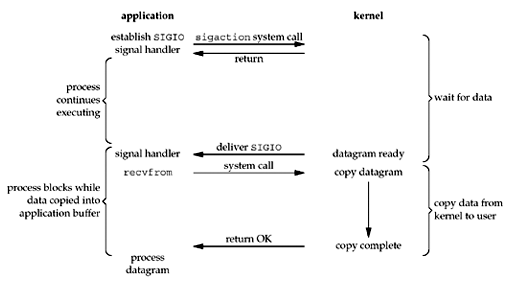
Signal-Driven I/O

该模型特点是第一阶段调用sigaction函数非阻塞返回，在第一阶段完成后发送信号SIGIO至进程，之后在signal handler中进行第二阶段处理。相当于对Nonblocking I/O Model的一种改进。

Asynchronous I/O Model

Asynchronous I/O Model相比较Signal-Driven I/O Model的区别在于通知的时机不同：Asynchronous I/O Model在第一和第二阶段都完成时通过信号通知进程操作完成。

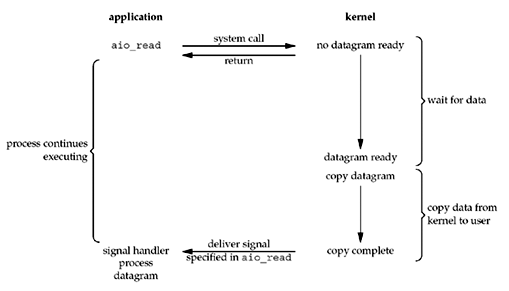
Asynchronous I/O Model

Asynchronous I/O Model对应java中AsynchronousSocketChannel，AsynchronousServerSocketChannel 和 AsynchronousFileChannel等api。

各个模型比较

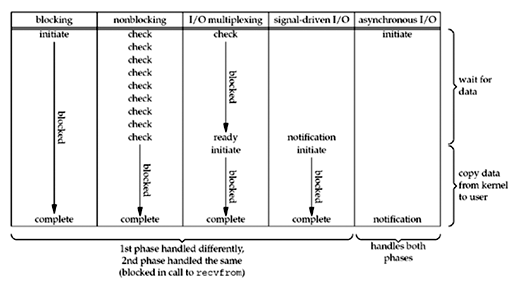
[1]: https://notes.shichao.io/unp/ch6/ “Chapter 6. I/O Multiplexing: The select and poll Functions”

2019-05-17发表2026-03-08更新工作 / 挑战6 分钟读完 (大约888个字)

[项目] 根据权限查询时避免角色切换遇到的坑

前情概要

1. 问题背景

使用多个角色查询列表时，会遇到两个维度的不同点：

行维度：多个角色能够看到行的并集，sql需要多次查询取并集，之后还要去重分页排序
列维度：如果不同角色可见列不同，计算出当前行能看到列的并集

举一个例子：

假设存在一个登录员工拥有两个角色：

长期激励负责人：能看到拥有长期激励的人（行维度），能看到基本信息和长期激励信息（列维度）
薪酬负责人：能看到低职级的人（行维度），能看到基本信息和薪酬信息（列维度）

那么，在列表中他能看见：

	基本信息	薪酬信息	长期激励信息
低职级/无长期激励	√	√	x
低职级/长期激励	√	√	√
高职级/无长期激励	x	x	x
高职级/长期激励	√	x	√

2. 实际遇到的问题（困难重重）

基本思路已经在前期概要里介绍，本人已经实践了一段时间，挖了两个深坑正在解决中。

性能问题（已解决）

最开始的实现中数据是一条一条读取的，同时薪酬字段属于加密信息，使用了第三方微服务提供解密，读取字段多+解密字段多导致了在百条分页的情况下接口在超时的边缘不断试探。。。

解决方案：

合并查询sql,批量查询数据
合并解密请求,批量调用解密微服务

因为之前为了方便我们解密使用了mybatis的TypeHandler做到字段隐式加解密，目前我们的做法是对于单条数据的加解密，还是保持原来的typeHandler做法，而对批量数据处理，重新写一套数据实体，同时使用mybatis的拦截器对查询的批量数据做批量解密的处理。具体做法可以参见我的另一片文章：【片段】 Mybatis ResultSetHandler 实践-续

批量查询带来的问题

批量查询返回的列表中列字段都是一致的，而我们的需求是不同的行能看见不同的列字段，把批量查询出来的列表直接返回是有问题的，这个问题因为疏忽导致了线上的一次故障。

所以目前的思路是先做一次数据批量预取，之后在对列字段做处理，隐藏掉不能看见的字段。

3. 总结

没有想到当时想解决权限查询时避免角色切换这个问题时会遇到这么多困难，想法是正确的，在实际执行时还是困难重重。值得欣慰的在最开始的时候思路和方向都是正确的，同时也把其中遇到的各种问题和心得记录了下来，经过层层积累，才到达现在的高度。

2019-04-18发表2026-03-08更新中间件 / resilience4j3 分钟读完 (大约431个字)

resilience4j-retry源码阅读

resilience4j 源码还是比较清晰简单的，比较适合阅读。

放一张主要类的结构图：

Retry入口

Retry接口是提供重试功能的入口，主要提供了方法模版，具体校验结构，失败后处理由Context子类实现。

/**
 * Creates a retryable supplier.
 *
 * @param retry    the retry context
 * @param supplier the original function
 * @param <T>      the type of results supplied by this supplier
 * @return a retryable function
 */
static <T> Supplier<T> decorateSupplier(Retry retry, Supplier<T> supplier) {
	return () -> {
		Retry.Context<T> context = retry.context();
		do try {
			T result = supplier.get();
			final boolean validationOfResult = context.onResult(result);
			if (!validationOfResult) {
				context.onSuccess();
				return result;
			}
		} catch (RuntimeException runtimeException) {
			context.onRuntimeError(runtimeException);
		} while (true);
	};
}

这里摘抄了一段核心代码，作用是循环直到context.onResult(result)返回true为止，需要留意context.onResult/onRuntimeError/onError可能执行多次， onSuccess只会执行一次，这里每次进入重试都是一个新的context对象。

Retry.ContextImpl

public boolean onResult(T result) {
    if (null != resultPredicate && resultPredicate.test(result)) {
        int currentNumOfAttempts = numOfAttempts.incrementAndGet();
        if (currentNumOfAttempts >= maxAttempts) {
            return false;
        } else {
            waitIntervalAfterFailure(currentNumOfAttempts, null);
            return true;
        }
    }
    return false;
}

public void onRuntimeError(RuntimeException runtimeException) {
    if (exceptionPredicate.test(runtimeException)) {
        lastRuntimeException.set(runtimeException);
        throwOrSleepAfterRuntimeException();
    } else {
        failedWithoutRetryCounter.increment();
        publishRetryEvent(() -> new RetryOnIgnoredErrorEvent(getName(), runtimeException));
        throw runtimeException;
    }
}

先关注onResult，它负责判断是否需要继续重试，如果通过校验或者重试超过此数，会停止重试。

onRuntimeError/onError, 负责把catch的异常存储在lastRuntimeException中。

public void onSuccess() {
	int currentNumOfAttempts = numOfAttempts.get();
	if (currentNumOfAttempts > 0) {
		succeededAfterRetryCounter.increment();
		Throwable throwable = Option.of(lastException.get()).getOrElse(lastRuntimeException.get());
		publishRetryEvent(() -> new RetryOnSuccessEvent(getName(), currentNumOfAttempts, throwable));
	} else {
		succeededWithoutRetryCounter.increment();
	}
}

onSuccess负责统计和发送事件。

总结

总体来说retry比较简单，需要注意的点有一个如果设置了结果校验，如果一直校验不通过，将返回未通过的结果，而不是返回失败。

缓存分类

缓存的不足

LeetCode两个经典的排序算法

最近这个季度

计划和休息

这边年读书情况

多角色权限如果遇到不同角色能看到不同的列可以怎么做

批量读取

树的高度

平衡树

两节点的最长路径

翻转树

归并两棵树

判断路径和是否等于一个数

统计路径和等于一个数的路径数量

子树

树的对称

最小路径

统计左叶子节点的和

间隔遍历

找出二叉树中第二小的节点

二叉树的层平均值

找树左下角的值

非递归实现二叉树的后序遍历

非递归实现二叉树的前序遍历

非递归实现二叉树的中序遍历

操作系统IO模型与Java IO

最基础的知识

Blocking I/O Model

Nonblocking I/O Model

I/O Multiplexing Model

Signal-Driven I/O Model

Asynchronous I/O Model

各个模型比较

1. 问题背景

2. 实际遇到的问题（困难重重）

性能问题（已解决）

批量查询带来的问题

3. 总结

Retry入口

Retry.ContextImpl

总结

链接

分类

最新文章

归档

标签